About vector databases
Vector databases enable LLM use cases that require efficient similarity search, including Retrieval-Augmented Generation (RAG) and AI agents.
Regardless of the database product you use, there are certain concepts that are common to all vector databases. Understanding these concepts will help you work with vector data in DataStax Enterprise (DSE).
What is RAG?
RAG is a technique for improving the accuracy of an LLM by adding relevant content directly to the LLM’s context window. Here’s how RAG works:
-
Pick an embedding model to generate embeddings from your data, and then store those embeddings in a vector database.
-
When the user submits a query, use the same model to generate an embedding from the user’s query, and then run a vector search to find data that’s similar to the user’s query.
-
Pass this data to the LLM so it’s available in the context window.
-
When the LLM generates a response, it is less likely to hallucinate (generate answers that sound or look correct but are actually incorrect).
To learn how to implement RAG, see the RAG demos on the DataStax Developers YouTube channel and the DataStax Enterprise (DSE) RAG example.
What are AI agents?
An AI agent provides an LLM with the ability to take different actions depending on the goal. In the preceding RAG example, a user might submit a query unrelated to your content. You can build an agent to take the necessary actions to fetch relevant content.
For example, you might design an agent to run a Google search with the user’s query. It can pass the results of that search to the LLM’s context window. It can also generate embeddings, and then store both the content and the embeddings in a vector database. In this way, your agent can build a persistent memory of the world and its actions.
Embeddings
Embeddings are vectors, often generated by machine learning (ML) models, that capture semantic relationships between concepts or objects. Related objects are positioned close to each other in the embedding space.
Learn more about embeddings and vectors
The process of generating embeddings transforms data (such as text or images) into vectors.
Vectors are numerical representations of data in relationship to other data in the same space. The set of vectors for an entire collection of data is the embedding.
Vectors are like individual addresses, and the embedding is a map of an entire neighborhood or city. By comparing vectors, an ML model can understand the degree of similarity of the data.
For a more detailed introduction to embeddings, see What is vector embedding.
To support vector search in a Cassandra-based database, vectors are stored as the VECTOR type in a vector field with a fixed dimensionality.
The dimensionality refers to the number of floats in the vector, which could be represented as VECTOR<FLOAT, 768>.
The dimension value is defined by the embedding model that you use.
Preprocess embeddings
You can use feature scaling or data normalization to prepare your data before you use it to train a model. Feature scaling balances or scales vectors consistently so that no one feature of your data unintentionally outweighs others.
Normalizing and standardizing are two feature scaling methods that you can use to preprocess your embeddings before writing them to a database. The method you use depends on factors like algorithm or data type.
| Method | Mathematical definition | Features |
|---|---|---|
Normalizing |
Scale data to a length of one by dividing each element in a vector by the vector’s length, which is also known as its Euclidean norm or L2 norm. Normalized datasets always range from 0 to 1. |
|
Standardizing |
Shift and scale data for a mean of zero and a standard deviation of one. Standardized datasets always have a mean of 0 and a standard deviation of 1. They can also have any upper and lower values. |
|
|
If embeddings are not normalized, the dot product silently returns meaningless query results. When you use OpenAI, PaLM, or Simsce to generate your embeddings, they are normalized by default. If you use a different library, you may need to normalize your vectors to use the dot product. |
Chunking
Chunking is a way to prepare your data for use in ML apps.
Chunking is the process of breaking up large, usually contiguous blocks of data into smaller pieces. For example, instead of generating an embedding for one large paragraph of text, you could break the paragraph into 150 character chunks.
Each chunk then has its own embedding, rather than a single embedding for the entire paragraph.
In your vector database, you insert the embedding for each chunk as a separate row in a table or document in a collection. To tie related chunks together, you insert static metadata with each chunk from the same original source. For example, if you break a product description into chunks, you might insert metadata like the product name, SKU, and other identifiers.
Chunking can help control costs because you pass fewer, more relevant objects to the LLM.
For more information about chunking, see RAG Cookbook: Chunking.
Embedding models
Embedding models translate data into vectors.
It’s important to select an embedding model for your dataset that creates good structure and ensures related objects are near each other in the embedding space.
For accurate vector search, you must must use the same embedding model for your data and your query vectors.
Embedding models process data differently, and some models are better suited to certain data types. You may need to test different embedding models to find the best one for your needs.
Many embedding models are available, and new models are released regularly.
Embedding providers, such as OpenAI and Hugging Face, are embeddings services that you can use to generate embeddings for your data.
Similarity metrics
Similarity metrics compute the similarity of two vectors.
Vectors, such as those produced by embedding algorithms, inherently reflect similarity. Similar items, such as two pieces of related text, result in embedding vectors that are similar, or near, to each other.
During a vector search, a query vector is compared against the vectors in the database. The search results represent the pieces of data, such as text or images, that are most relevant to the query vector.
Vector search results are based on similarity scores, which are calculated using a similarity metric.
Cassandra-based databases support three types of similarity metrics:
|
Cosine and dot product are equivalent for vectors normalized to unit norm. However, if your embeddings are not normalized, then don’t use dot product because it will silently give you nonsense in query results. |
Cosine metric
When the metric is set to cosine, a vector database uses cosine similarity to determine the closeness (similarity) of two vectors.
Cosine similarity compares the direction that two vectors point towards, and it ignores their length (also known as the norm). For this reason, cosine doesn’t require vectors to be normalized.
This computation results in a value between 0 and 1 for each set of vectors, where 1 represents maximal similarity (vectors that point in the exact same direction).
Mathematical details for cosine similarity
Given two vectors A and B, their cosine similarity is computed based on the dot product of the vectors divided by the product of their magnitudes (norms). The formula for cosine similarity is:
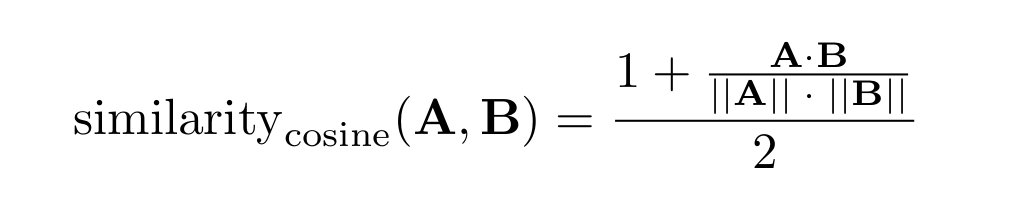
Where:
-
A ⋅ B is the dot product of vectors A and B (see Dot product for a defining formula).
-
∥A∥ is the magnitude (norm) of vector A.
-
∥B∥ is the magnitude (norm) of vector B.
The resulting similarity score, ranging from 0 to 1, indicates how close (similar) one vector is to another:
-
A value of 0 indicates that the vectors are diametrically opposed, having the same direction but opposite sense, regardless of their magnitude.
-
A value of 0.5 denotes that the vectors are orthogonal (perpendicular) to each other.
-
A value of 1 indicates that the vectors are identical in both direction and sense, but they do not have necessarily the same magnitude.
Dot product metric
When the metric is set to dot_product, a vector database uses the dot product to determine the closeness (similarity) of two vectors.
The dot product algorithm is about 50% faster than cosine, but it requires vectors to be normalized to unit norm to give meaningful results. Although most embedding models yield normalized vectors, it is a best practice to verify before switching to this similarity metric.
Mathematical details for dot product similarity
Consider two vectors A and B of dimension d. Expressed with their numeric component, these look like:
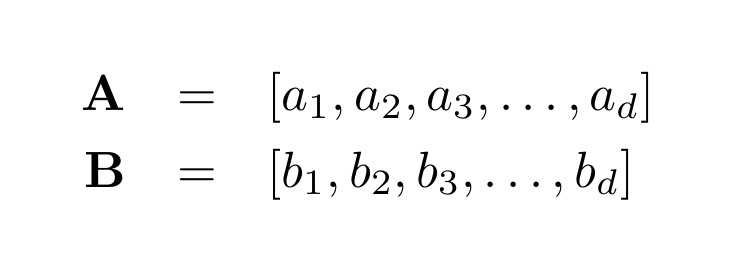
Their dot product is calculated as follows:
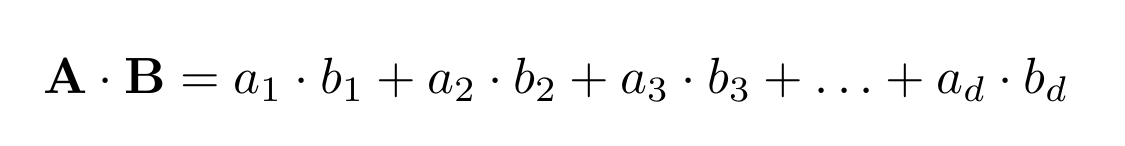
The dot product gives a scalar result (a number). This has important geometric implications: If the dot product is zero, then the two vectors are orthogonal (perpendicular) to each other. When the vectors are normalized to unit norm, the dot product represents the cosine of the angle between them and is always between -1 and +1.
The dot product similarity, built on the above, applies the same rescaling as for the cosine case:
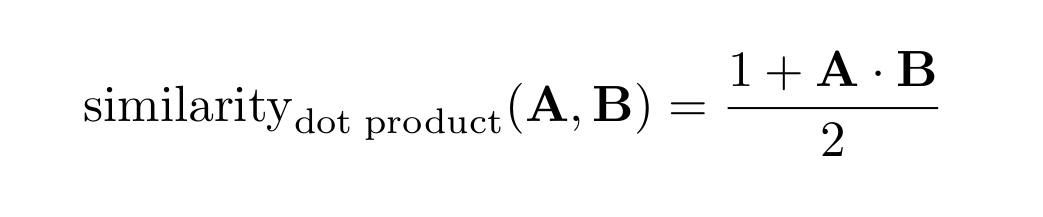
The dot product similarity is designed to work like cosine similarity for the special case of vectors with unit norm. In practice, dot product doesn’t divide by the vectors' norm, which is supposedly equal to one, and this saves a fair amount of CPU. For vectors of arbitrary norm, however, the outcome is unpredictable and might not even be bound in any finite numeric range.
In the context of a vector database, the dot product similarity yields the same results as the cosine similarity, as long as the vectors have unit norm. In other words, if you compute the dot product similarity of two normalized vectors, you get their cosine similarity. In this case, dot product is to be preferred because it computationally faster.
Euclidean metric
When the metric is set to euclidean, the database uses the Euclidean distance to determine the closeness (similarity) of two vectors.
The Euclidean distance is the most common way of measuring the ordinary, straight-line distance between two points in Euclidean space.
Mathematical details for Euclidean similarity
Given two vectors A and B in a d-dimensional space, expressed in components as
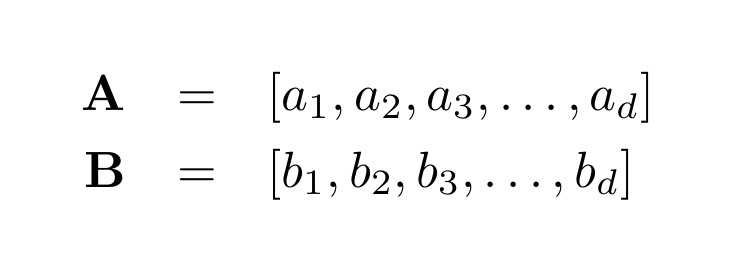
the Euclidean distance between them is defined by the relation:
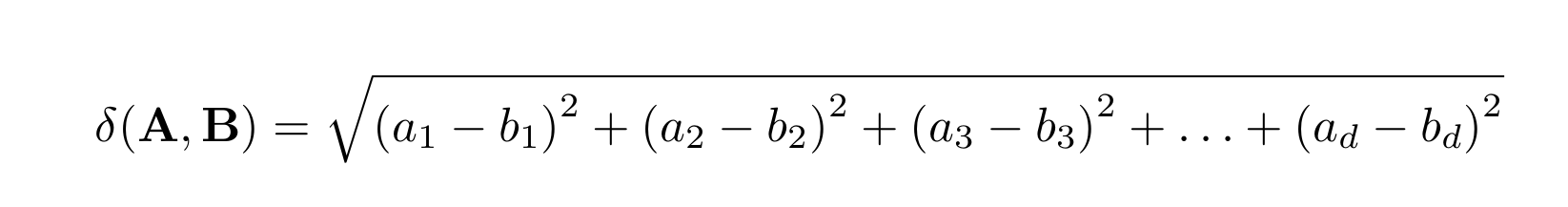
The Euclidean similarity is derived from the Euclidean distance through the following formula:
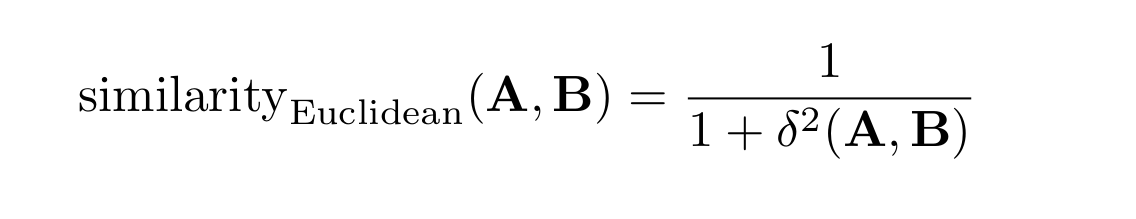
The Euclidean similarity, based on the Euclidean distance, increases as the distance decreases.
In order to lie in the zero-to-one interval, and to increase as the distance decreases, Euclidean similarity features an inverse relationship with the (squared) distance, as well as a cutoff value to prevent an explosion to infinity when the two vectors approach each other.
As the Euclidean distance increases from zero to infinity, the Euclidean similarity decreases from one to zero. For vectors normalized to one, the Euclidean distance always lies between zero and two: correspondingly, the similarity never drops below one-fifth.
In the context of a vector database, the following apply:
- Vectors as points
-
Each vector in the database can be thought of as a point in some high-dimensional space.
- Distance between vectors
-
When you want to find how close two vectors are, the Euclidean distance is one of the most intuitive and commonly used metrics.
If two vectors have a small Euclidean distance between them, they are close in the vector space, and therefore similar according to Euclidean similarity. If they have a large Euclidean distance, they are far apart, and therefore dissimilar.
- Querying and operations
-
When you set the metric to
euclidean, your vector database uses the Euclidean distance as the metric for any operations that require comparing vectors. For example, a similarity search returns vectors that have the smallest Euclidean distance to the query vector.
Vector search
At its core, a vector database is about efficient similarity search, which is also known as vector search. Vector search finds content that is similar to a given query.
Here’s how vector search works:
-
Generate an embedding for a new piece of content outside the original collection. For example, you could generate an embedding from a text query submitted by a user to a chatbot.
Make sure you use the same embedding model for your original embeddings and your new embedding.
-
Use the new embedding to run a vector search on the collection and find data that is most similar to the new content.
Mechanically, a vector search determines the similarity between a query vector and the vectors of the documents in a collection. Each document’s resulting similarity score represents the closeness of the query vector and the document’s vector.
-
Use the returned content to produce a response or trigger an action in an LLM or GenAI application. For example, a support chatbot could use the result of a vector search to generate an answer to a user’s question.
Limitations of vector search
While vectors can replace or augment some functions of metadata filters, vectors are not a replacement for other data types. Vector search can be powerful, particularly when combined with keyword filters, but it is important to be aware of its limitations:
-
Vectors aren’t human-readable. They must be interpreted by an LLM, and then transformed into a human-readable response.
-
Vector search isn’t meant to directly retrieve specific data. By design, vector search finds similar data.
For example, assume you have a database for your customer accounts. If you want to retrieve data for a single, specific customer, it is more appropriate to use a filter to exactly match the customer’s ID instead of a vector search.
-
Vector search is a mathematical approximation. By design, vector search uses mathematical calculations to find data that is mathematically similar to your query vector, but this data may not be the most contextually relevant from a human perspective.
For example, assume you have database for a department store inventory. A vector search for
green hiking bootscould return a mix of hiking boots, other types of boots, and other hiking gear.Use metadata filters to narrow the context window and potentially improve the relevance of vector search results. For example, you can improve the
hiking bootsvector search by including a metadata filter likeproductType: "shoes". -
The embedding model matters. It’s important to choose an embedding model that is ideal for your data, your queries, and your performance requirements. Embedding models exist for different data types (such as text, images, or audio), languages, use cases, and more.
Using an inappropriate embedding model can lead to inaccurate or unexpected results from vector searches. For example, if your dataset is in Spanish, and you choose an English language embedding model, then your vector search results could be inaccurate because the embedding model attempts to parse the Spanish text in the context of the English words that it was trained on.
Additionally, you must use the same model for your stored vectors and query vectors because mismatched embeddings can cause a vector search to fail or produce inaccurate results.
Approximate nearest neighbor
Cassandra-based databases support only Approximate Nearest Neighbor (ANN) vector searches, not exact K-Nearest Neighbor (KNN) searches.
ANN search finds the most similar content within reason for efficiency, but it might not find the exact most similar match. Although precise, KNN is resource intensive, and it is not practical for applications that need quick responses from large datasets. ANN balances accuracy and performance, making it a better choice for applications that query large datasets or need to respond quickly.
To learn more about ANN and KNN, see What is the k-nearest neighbors (KNN) algorithm.
Indexing
Databases based on Apache Cassandra® provide numeric-, text-, and vector-based indexes to support different kinds of searches. You can customize indexes based on your requirements, such as specific similarity functions or text transformations.
Storage-Attached Indexing (SAI) is a highly-scalable, globally-distributed index for Cassandra databases. With SAI, searches can efficiently find rows that satisfy query predicates. It is ideal for large datasets, particularly those that must support vector search.
When you run a search, SAI loads a superset of all possible results from storage based on the predicates you provide.
SAI evaluates the search criteria, sorts the results by vector similarity, and then returns the top limit results to you.
SAI uses the JVector Approximate Nearest Neighbor (ANN) search algorithm for similarity search. By design, ANN prioritizes speed and efficiency over exact accuracy. Taking inspiration from DiskANN, JVector balances speed and accuracy by creating a hierarchy of navigable graph indexes. All data points, or nodes, on the graph, can find a path to any other node.
When you insert data, JVector adds those new documents to the graph immediately, so you can efficiently search right away.
To save space and improve performance, JVector can compress vectors with quantization.
For more information about indexing, see Cassandra Query Language (CQL) reference: Storage-Attached Indexing
